Вітаю вас на лабораторній роботі №5

5.1 Теоретичні відомості.

Грубі похибки. Часто причинами неточностей є помилки оператора при вимірюванні, такі як неправильнa точка відліку за шкалою вимірювального пристрою, неправильна запис результату спостереження або неправильна фіксація окремих значень. Також можуть виникати повторювані помилки при використанні приладів. Втім, грубі похибки можуть мати більш серйозні причини, такі як раптові зміни умов вимірювання або несправності в апаратурі, які можуть залишитися непоміченими.

Виявлення та виключення грубих похибок. Для виявлення грубих похибок вимірювання використовують методи математичної статистики, зокрема, статистичну перевірку гіпотез. Цей метод полягає у висуненні нульової гіпотези про результат вимірювання, який викликає сумнів, і перевірці його на практичну неймовірність за допомогою статистичних критеріїв. Якщо нульова гіпотеза не може бути спростована з визначеною рівнем значущості ймовірністю, то промах виключають, а якщо ні - результат залишають. Вибір критерію перевірки ґрунтується на практичній впевненості, для якої задається рівень значущості. Якщо значення критерію перевірки потрапляє в критичну область, то нульову гіпотезу відкидають.

Критерії грубих похибок. Відомий ряд критеріїв, які дозволяють виключити грубі промахи. До них, зокрема, можна віднести критерій Греббса (Смирнова), Шарлье, Шовене, Діксона та ін. Ці критерії засновані на статистичних оцінках параметрів розподілу, так як в більшості випадків дійсні значення параметрів розподілу невідомі.

Критерій Шарльє

Краще використовувати критерій Шарльє для рядів вимірювань з числом спостережень понад 20. Згідно з теоремою Бернуллі, якщо кількість результатів вимірювання перевищує 20, то кількість результатів, що за абсолютним значенням перевищують Kш , буде дорівнювати [I - Ф(Кш)].

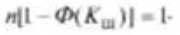
Звідси Кш =

Критичні значення критерію Шарлье можна визначити за формулою:

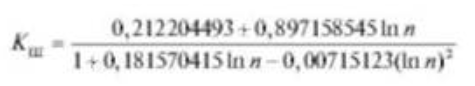
(для 5 < п < 100, /> = 0,95.)

Користуючись критерієм Шарлье, відкидають результат, значення якого перевершує по модулю

Порядок виявлення і виключення грубих похибок і промахів з використанням критерію Шарлье зводиться до наступного:

• Визначається середнє значення результатів вимірювання.
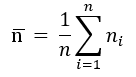
• Визначається оцінка середнього квадратичного відхилення.
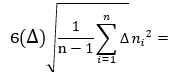
• Визначається розрахункове (критичне) значення критерію Шарлье по рівнянню
• Визначається абсолютне значення різниці сумнівного результату
• Порівнюються значення

5.2 Хід роботи

5.2.1 Зняти покази з цифрового тахометра та занести дані у відповідну таблицю.

5.2.2 Обчислити середньоарифметичне результатів спостереження. Воно в подальшому буде прийнято за дійсне значення,або за результат вимірювання швидкості обертання. Істинним значенням швидкості обертання двигуна є математичне очікування.

5.2.3 Визначити відхилення дійсного значення (середнього арифметичного) швидкості обертання двигуна від математичного очікування (істинного значення) швидкості обертання двигуна.

5.2.4 Визначити ередньоквадратичне відхилення, результатів спостереження від середньоарифметичного.

5.2.5 Розраховати довірчий інтервал для результатів спостереження.

5.2.6 Перевірка на наявність грубої похибки у результатах спостережень.

5.2.7 Визначити довірчі інтервали.

5.2.8 Виключити грубу похибку та повторити пункти 5.2 - 5.6.

5.2.9 Розрахувати швидкість обертання двигуна та зробити висновки.